Input consists of a hypothesis matrix and a raw or correlation data matrix. Input files should be in headerless, comma-separated (.csv) format. The "CSV Generator" in the header bar is a web application for creating properly-formatted correlation and hypothesis matrices.
Here are five lines from a possible raw data file:
1.24,2.61,0.260,1.05,7.55,0.2 0.280,2.36,1.19,1.66,0.470,0.460 0.370,0.820,3.23,0.120,4.57,1.84 0.110,5.73,3.04,1.04,0.380,0.350 0.750,2.66,2.62,0.290,4.12,0.380
Each row is a participant or observation, and each column is a variable. Note the absence of an ID column, which would be interpreted as a variable.
Here is a sample correlation data file:
1.0 0.2,1.0 0.3,0.4,1.0
Data from the upper half of the correlation matrix is optional. In SPSS, you can produce a plain correlation matrix such as this using the following syntax:
FACTOR /VARIABLES v1 v2 v3 /MISSING LISTWISE /ANALYSIS v1 v2 v3 /PRINT CORRELATION /ROTATION NOROTATE /METHOD=CORRELATION
Here is a sample hypothesis file:
2,1,1,0 3,1,1,0 3,2,0,0.2 4,1,2,0
Each row of the hypothesis matrix is of the form: row, column, parameter tag, fixed value. The first two columns specify a correlation, conventionally from the lower half of the correlation matrix, and the third and fourth make an assertion about the value of that correlation. Correlations with the same positive integer in the parameter tag column are hypothesised to be equal, and correlations with a parameter tag of 0 are hypothesised to be equal to the value of their fixed value column. Correlations with different parameter tags are not hypothesised to be unequal. If a parameter tag is assigned to a single correlation then the output will include an estimate of that correlation, but the p value for the test will be the same as if it hadn't been included.
You can also use an MML-WBCORR (see the header bar) style hypothesis file, which has a group column at the beginning of the matrix. Since MML-Multicorr is restricted to the one group case, this merely adds a column of ones to the beginning of the matrix. This is what the above hypothesis would look like in the CSV Generator, which uses WBCORR format:
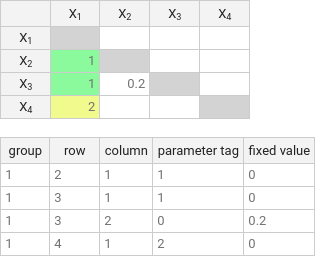
Let's break down this hypothesis. The first two columns specify the correlation at row 2 of column 1 (ρ21). Put differently, they pick out the correlation between variable 2 and variable 1. This correlation has a parameter tag of 1, so it is hypothesised to be equal to the correlation picked out by the second row, which also has a parameter tag of 1. On the other hand, the correlation in the third row, since its parameter tag is 0, is hypothesised to be equal to 0.2. Finally, the correlation identified by the fourth row is the only correlation with a parameter tag of 2, so it does not figure into the hypothesis at all. Effectively, the hypothesis says: (ρ21 = ρ31) & (ρ32 = 0.2).
A parameter tag column has a "hole" in it if the value of the greatest parameter tag is not equal to the number of unique non-zero parameter tags. For example, if the parameter tag column were [1, 1, 2, 2, 4, 4], then it would have a hole because 3 is skipped. If the column has a hole then it is renumbered, in this case to [1, 1, 2, 2, 3, 3]. This does not affect the result of the test, and the amended hypothesis matrix is included in the output.
The estimation methods offered by MML-Multicorr are GLS (generalised least squares), ADF (asymptotically distribution-free), and a "two-step" version of each (TSGLS and TSADF). The practical difference between GLS and ADF is that whereas GLS assumes multivariate normality, ADF does not. However, ADF relies on sample estimates of fourth-order moments, so it requires raw data and is incompatible with pairwise deletion. Also, since these estimates have large standard errors for small to moderate sample sizes, employing ADF may result in a considerable loss of power: it should only be used if the assumption of multivariate normality is untenable. A test of multivariate normality is provided when you use raw data. The relation between TSGLS and TSADF is the same, but that they provide superior estimates compared to their one-step counterparts.
In brief: use TSGLS if multivariate normality is a tenable assumption, and use TSADF otherwise.
Listwise and pairwise deletion are offered to deal with missing data. In pairwise deletion, the sample size is the harmonic mean of the number of observed scores for each variable, rounded to one decimal place. Empty or NA values (and only empty or NA values) are interpreted as missing.
This page will interpret the output for an example data set. The first table in the output is the hypothesis matrix:
| Input Hypothesis Matrix | ||||
| Group | Row | Column | Parameter Tag | Fixed Value |
|---|---|---|---|---|
| 1 | 2 | 1 | 1 | 0 |
| 1 | 3 | 1 | 1 | 0 |
| 1 | 3 | 2 | 1 | 0 |
The hypothesis asserts that ρ21 = ρ31 = ρ32. Next we see the correlation matrix:
| Input Correlation Matrix (N=25) | ||||||
| X1 | X2 | X3 | X4 | X5 | X6 | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0.109 | 0.007 | -0.074 | 0.196 | -0.116 |
| X2 | 0.109 | 1 | 0.077 | -0.067 | 0.107 | -0.239 |
| X3 | 0.007 | 0.077 | 1 | 0.129 | 0.15 | -0.069 |
| X4 | -0.074 | -0.067 | 0.129 | 1 | -0.152 | -0.193 |
| X5 | 0.196 | 0.107 | 0.15 | -0.152 | 1 | -0.323 |
| X6 | -0.116 | -0.239 | -0.069 | -0.193 | -0.323 | 1 |
| OLS Estimates Matrix (N=25) | ||||||
| X1 | X2 | X3 | X4 | X5 | X6 | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0.064 | 0.064 | -0.074 | 0.196 | -0.116 |
| X2 | 0.064 | 1 | 0.064 | -0.067 | 0.107 | -0.239 |
| X3 | 0.064 | 0.064 | 1 | 0.129 | 0.15 | -0.069 |
| X4 | -0.074 | -0.067 | 0.129 | 1 | -0.152 | -0.193 |
| X5 | 0.196 | 0.107 | 0.15 | -0.152 | 1 | -0.323 |
| X6 | -0.116 | -0.239 | -0.069 | -0.193 | -0.323 | 1 |
The OLS matrix is null-consistent, so since the observed values of ρ21, ρ31, and ρ32 are 0.109, 0.007, and 0.077, and since those three are equal under the null hypothesis, therefore their OLS estimate is (0.109 + 0.007 + 0.077)/3 = 0.064.
Next we have the GLS, TSGLS, ADF, or TSADF parameter estimates, depending on which method was selected at input:
| TSGLS Parameter Estimates | |||
| Parameter Tag | Estimate | Standard Error | 95% Confidence Interval |
|---|---|---|---|
| 1 | 0.067 | 0.015 | [-0.337, 0.45] |
The TSGLS estimate is parameter 1 = ρ21 = ρ31 = ρ32 = 0.067. As with the OLS matrix, this is a null-consistent estimate. This table also contains 95% confidence intervals on point estimates, using a strict Bonferroni. Confidence intevals are calculated using the Fisher transform method.
Next we have the significance of the hypothesis test:
| Significance Test Results | ||
| Chi Square | df | plevel |
|---|---|---|
| 0.147 | 2 | 0.929 |
And finally, since we used raw data, we have the test of multivariate normality. The specific test will depend on 1) whether there is missing data and 2) which deletion method was employed. Yuan, Lambert & Fouladi's (2004) test is given if pairwise deletion was chosen, and Mardia's (1970) is provided otherwise. Yuan, Lambert & Fouladi's (2004) test is only useable if the observed marginals of the incomplete variables do not sit in a restricted range, and a test of that assumption is provided as well. This is only possible if there is at least one variable without missing data.
Since the example data is complete, Mardia's (1970) test is given:
| Assessment of Multivariate Skewness | ||||
| Group | Multivariate Skewness | Chi Square | df | plevel |
|---|---|---|---|---|
| 1 | 27.396 | 114.151 | 56 | < 0.001 |
| Assessment of Multivariate Kurtosis | |||
| Group | Multivariate Kurtosis | Z statistic | plevel (2-tailed) |
|---|---|---|---|
| 1 | 55.168 | 2.771 | 0.006 |
Since the p value is low for both the skewness test and the kurtosis test, multivariate normality is not supported and we should rerun the test using TSADF.
Suppose we remove one value from the data set and choose pairwise deletion. Now Yuan, Lambert, and Fouladi's (2004) test is displayed. This begins with an assessment of the distribution of the observed marginals:
| Assessment of the Distribution of the Observed Marginals | ||||
| Group | Variable | Missing values | ZR | plevel (two-tail) |
|---|---|---|---|---|
| 1 | 1 | 1 | -0.416 | 0.677 |
The p value is high, so the range of the observed marginals does not appear to be restricted and we can move on to the assessment of multivariate normality:
| Assessment of Multivariate Normality | ||
| Group | M2 | plevel (two-tail) |
|---|---|---|
| 1 | -2.468 | 0.014 |
Again the p value is low, so multivariate normality is not supported and we should re-run the test using TSADF.
MML-Multicorr is a application implementation of procedures to addres the TYPES of research questions addressed with Multicorr -- a correlation pattern hypothesis test program developed by Steiger (1979).
This About page is in development to clarify that except in specific cases, in contrast with Steiger's Multicorr, MML-Multicorr procedures are based on the GLS, 2SGLS, ADF, 2SADF theory as implemented in MML-WBCORR, and has several additional functionalities from the program developed by Steiger (WBCORR, 1997). These additional functionality and should be described here.
Please also refer to http://www.sfu.ca/psychology/research/mml/resources.html
MML-Multicorr may be cited in APA style as follows:
Fouladi, R. T, & Serafini, P. E. (2018). MML-Multicorr. Retrieved from http://members.psyc.sfu.ca/labs/mml.
Offline and bootstrap versions of MML-Multicorr are available at its github page.